What is inhomogeneity?
A common “rookie” mistake in point pattern analysis is to reject CSR in favor of clustering, but without realizing that apparent clustering might actually be driven by inhomogeneity. Inhomogeneity is a form of first-order nonstationarity and refers to the violation of the assumption that the mean intensity of the point process is constant (or, more formally, “invariant under translation”). This does not imply that the count of points should be exactly the same in different test regions (such as quadrats), but that the counts are drawn from a distribution with the same mean intensity. A point process of constant mean intensity is said to be “homogeneous”; if the mean intensity varies, the point process is said to be “inhomogeneous”. Note that almost all basic tests of independence (including commonly used indices such as Clark-Evans and summary functions such as Ripley’s K) assume homogeneity, where the null model is a homogeneous Poisson point process [a.k.a. complete spatial randomness (CSR)]. Conducting this type of test is often a first step in a point pattern analysis (a “dividing hypothesis”); if CSR is rejected in the direction of clustering, the point pattern is either clustered or inhomogeneous; the task then becomes determining between clustering and inhomogeneity. The problem is that identifying and testing for inhomogeneity can be tricky. The purpose of the present article is to raise awareness about inhomogeneity and to demonstrate some common ways to visualize and test for inhomogeneity.
The classic approach
The classic way to test for inhomogeneity is the chi-square test of uniformity. For a homogeneous Poisson point process, the expected count of points in a test region is equal to the area of the test region (i.e., the area of each quadrat) times the estimated intensity in the study area; the observed counts are then compared to expected counts via the Pearson chi-square statistic. The major disadvantage of this test is that the same procedure is also used to test for independence assuming homogeneity; the two can be easily confounded.
Modern approaches for visualizing and testing for inhomogeneity
For any sort of statistical analysis, the first step is always to look at the data. For point patterns, looking at the pattern itself can often provide the best clue as to whether the pattern is inhomogeneous. For example, below is a realization of a simulated inhomogeneous Poisson point process, where a one-unit change in the x-coordinate results in a fivefold increase in the intensity of the point pattern.

An inhomogeneous Poisson point pattern with a systematic trend in intensity. For a 1-unit change in the x-coordinate there is a fivefold increase in intensity.
It is easy to see that the intensity on the left side of the plot is substantially lower than the intensity on the right side of the plot, which is a clue that the point pattern is inhomogeneous. If a summary function (e.g., Besag’s L-function) were used to test the null hypothesis of CSR against the alternative that the point pattern is clustered, there is strong evidence against the null hypothesis in the direction of clustering, even though the result is being driven entirely by inhomogeneity and not clustering.
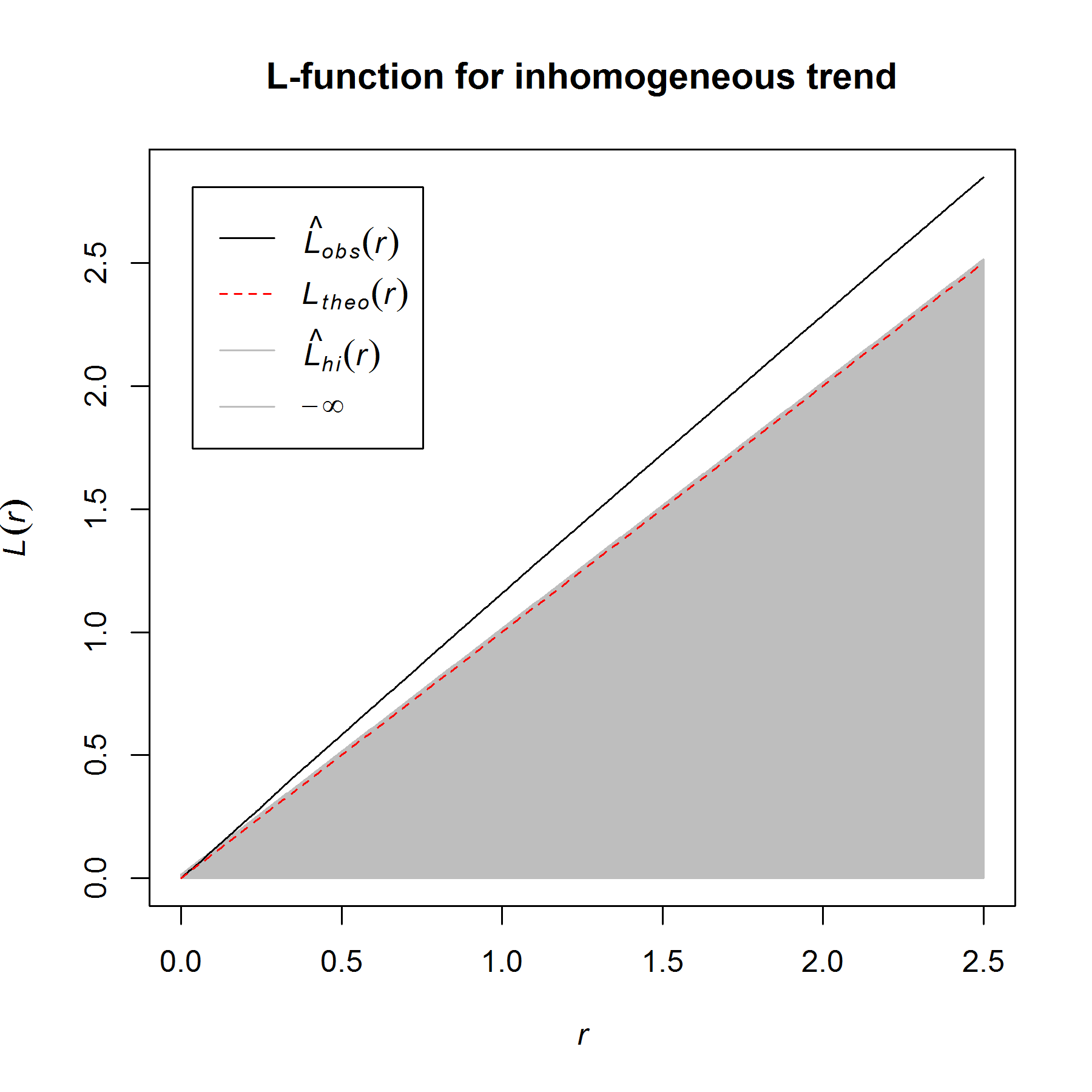
Besag’s L-function for the inhomogeneous point pattern with a trend in the intensity along the x-coordinate (shown above). A one-sided, simultaneous significance envelope was constructed based on 999 simulations of CSR with the same global intensity. Note that the summary function deviates above the envelope (in the direction of clustering) and provides strong evidence against the null hypothesis of CSR. The apparent clustering, however, is driven by inhomogeneity.
In other cases, inhomogeneity can be more difficult to identify visually, especially when the intensity of the point pattern is relatively low. For example, here are six realizations of a homogeneous Poisson point process with mean intensity equal to 0.5. Note that several of the point patterns (e.g., Simulation 1 and Simulation 3) may appear as if they were inhomogeneous, when (in fact) the underlying point process is homogeneous.
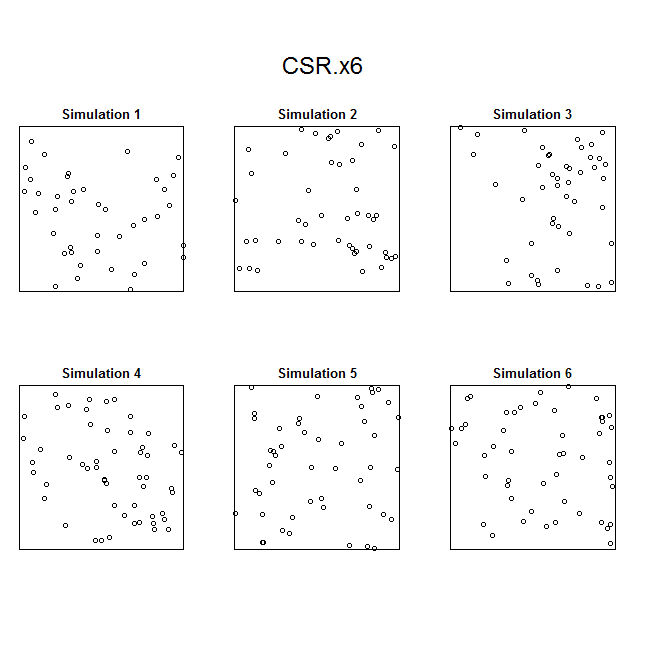
Six realizations of CSR with an itensity (lambda) of 0.5. Note that several of the point patterns (e.g., Simulation 1 and Simulation 3) appear as if they could be inhomogeneous when, in fact, the underlying process is homogeneous.
Another common way to visualize inhomogeneity is by kernel smoothing. This results in a raster surface where each cell represents the kernel smoothed local intensity of the point pattern. A Monte Carlo procedure can then be used to compare the maximum intensity of the observed point pattern to the maximum intensity for multiple realizations of CSR with the same global intensity. For example, below is the kernel smoothed intensity surface for a point pattern that represents the locations of gopher tortoise burrows in a pine stand. In this case the bandwidth (i.e., the standard deviation of the isotropic Gaussian kernel) was chosen via the default method in the ‘spatstat’, which is based on the dimensions of the study area window. Applying the Monte Carlo procedure described above resulted in a P-value of 0.11 and hence failure to reject the null hypothesis (at α = 0.05) of no difference between the observed maximum intensity and the expected maximum intensity under CSR. While kernel smoothing is a useful nonparametric method for visualizing the intensity surface, test results often vary depending on the method that is used to select the bandwidth. For example, when maximum likelihood cross-validation was used to select the bandwidth and the same Monte Carlo testing procedure was applied, the P-value was 0.012 and the null hypothesis was rejected.
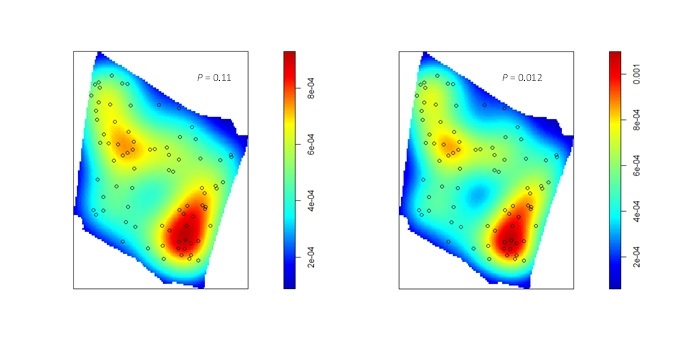
Kernel smoothed intensity surfaces for a point pattern representing the locations of gopher tortoise burrows (black circles) in a pine-stand. For the figure on the left, the default method in ‘spatstat’ was used to select the bandwidth (which is based on the dimensions of the study area window); for the figure on the right, maximum-likelihood cross-validation was used to select the bandwidth. For the intensity surface based on the default bandwidth selection method, the null hypothesis (that the maximum observed intensity was more extreme than that expected under CSR with the same global intensity) could not be rejected (P = 0.11). For the intensity surface where the bandwidth was selected based on maximum-likelihood cross-validation, the null hypothesis was rejected (P = 0.012). This example illustrates that sensitivity of methods based on nonparametric kernel smoothing to the chosen bandwidth.
Kernel smoothed intensity surfaces can also be problematic when they are used to estimate intensity for the purpose of correcting for it (e.g., when using something like an inhomogeneous K or L-function), and the results can often vary depending on which bandwidth is chosen. For example, if the intensity of the process is substantially higher in certain areas, using a kernel smoothed intensity surface as a source to correct for inhomogeneity often results in a summary function that seems to be under-corrected at short distances and over-corrected at longer distances (for a demonstration, see my other post on: “Significance envelope for cross-type summary function based on kernel-smoothed intensity surfaces”).
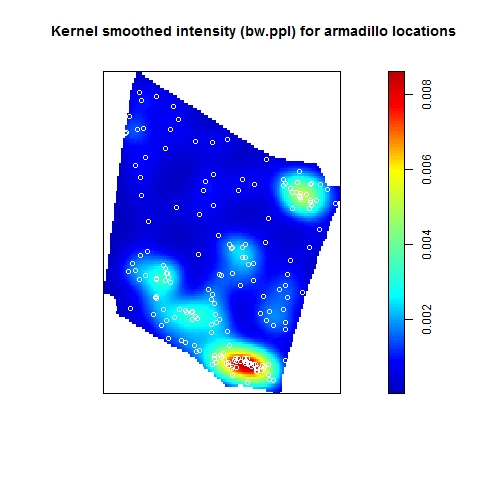
I have found that a useful way to assess if the kernel smoothed intensity surface is accurate is to simulate an inhomogeneous point pattern based on the kernel smoothed intensity surface. For example, below is a kernel smoothed intensity surface for armadillo burrows (found in the same study area as the gopher tortoise burrows shown above); the open white circles are the armadillo burrows. Much of the inhomogeneity in the distribution of armadillo burrows in this study area is associated with raised dirt berms that were created when the pine stand was windrowed, and on which the armadillos burrow intensively (as they prefer to burrow on sloped surfaces). Note that simulations based on this surface result in point patterns that do not closely resemble the observed point pattern; when the kernel smoothed surface is used to estimate the intensity surface, the intensity of the point pattern is lower than expected on the berms, but higher than expected in the vicinity of the berms.

Six realizations of an inhomogeneous Poisson point process based on the kernel smoothed intensity surface for armadillos (shown above). Note that the intensity of burrows is over-estimated in the vicinity of the berms.
If you want to examine whether the intensity of the point process is dependent on a single covariate, there are a handful of methods that can be used to both visualize and test for dependency, such as relative distribution estimation and various tests based on cumulative distribution functions. However, a more flexible approach (especially when you want to examine more than one potential covariate)
When possible, a better way to estimate the intensity function is by fitting a parametric point-process model, such as an inhomogeneous Poisson point-process model. There are other methods that exist for testing the effect of a covariate on intensity (such as methods involving cumulative distribution functions), but model fitting is superior because there is the potential to include more than one covariate. For the armadillo example, a binary mask was created from the GPS outlines of the berms and was used as a logical covariate; I then fit a model that is “homogeneous in different regions”: the point patterns on and off the berm are CSR, but differ in intensity. Based on the eyeball test, one can see that simulated point patterns based on this model more closely resemble the observed point pattern. Moreover, one can use an analysis of deviance table (with something like a likelihood ratio test) to compare the fit model with the logical covariate to a model with constant intensity; in this manner, model fitting provides a sensible way to test whether one can reject CSR in favor of an inhomogeneous model; in this case, there is strong evidence against CSR in favor of the model that includes the logical covariate (P < 0.001). For comparison, I have also simulated point patterns based on CSR; it is easy to see that these simulated point patterns do not resemble the observed point pattern.

Eight realizations of an inhomogeneous Poisson point process based on model fitting. The outline of the berms was traced with a GPS and then coverted into a binary mask that was used as a logical covariate in the log-linear model. Note that the simulated point patterns based on the model better represent the observed pattern.

Eight realizations of CSR based on the global intensity of the armadillo burrows in the stand. There was strong evidence against the model based on CSR in favor of the model with the logical covariate representing the area of the berms. The simulated point patterns shown here do not look anything like the observed pattern.
In most cases, estimating intensity from a parametric model works better than nonparametric kernel smoothing, but model fitting is only practical when the covariates driving the inhomogeneity can be mapped and accounted for. In the case of armadillo and gopher tortoise burrows in the above example, the point processes for armadillo and gopher tortoise burrows are independent, but the two species are choosing locations with subtle differences in microhabitat, the latter of which can be very difficult to map over a large area.
Summary and prospectus
In point pattern analysis, inhomogeneity can confound tests of independence, but is often unrecognized by novices because: 1) they are unaware of the problem and 2) many popular software packages do not have functionality to characterize and account for inhomogeneity. Even when such functionality exists, tests of inhomogeneity can be easily biased and it is not always clear how to characterize inhomogeneity so that it can be accounted for (e.g., using inhomogeneous summary functions). While there does not seem to be a simple solution to this problem, you should start by looking at your data and then calculating a simple summary function with an envelope test; rejection of null hypothesis of CSR in the direction of clustering would indicate that the potential for inhomogeneity should be explored further. Kernel smoothing can be a useful way to visualize inhomogeneity, but bandwidth selection can be tricky, and analysts should be careful when using such surfaces to correct for inhomogeneity because over-smoothing can distort intensity estimates when there are subregions with relatively high intensity. The best approach for estimating intensity (e.g., for the purpose of correction) is to fit a parametric model, but this may not be feasible if the underlying covariates are difficult to map.
Although inhomogeneity can make point pattern analysis more complicated, the emergence of methods that can account for inhomogeneity represents an exciting development in point pattern analysis because most point patterns are inhomogeneous.
Postface:
All of the analyses and figures above were created with the ‘spatstat’ package in R, along with ‘colorRamps’ (for the color scheme in the kernel surfaces) and ‘rgdal’ (for importing shapefiles).
The citation for ‘spatstat’ is:
Baddeley A, Turner R (2005). spatstat: An R Package for Analyzing Spatial Point Patterns. Journal of Statistical Software 12:1-42.
If you are interested in point pattern analysis, I highly recommend their companion book:
Baddeley A, Rubak E, Turner R(2015). Spatial Point Patterns: Methodology and Applications with R. London: Chapman and Hall/CRC Press.